行星运动方程

这其实是我高中很早时候好奇算过的一个东西，现在就顺手写出来吧

在高中学习万有引力定律时，我们采用的是一种简化的模型：将其考虑为匀速圆周运动，但我们仍对现实中行星运动真实的运动轨迹产生了浓厚的兴趣，因此我们小组对此开始了研究。
高中课本上使用的模型为,把一个大质量行星看做是固定的，另一个小质量天体是运动的，它们之间存在作用力：

$$F = \frac{GMm}{R^2}$$

因此由匀速圆周运动模型得到：

$$m\frac{v^2}{R}=\frac{GMm}{R^2}$$

现在我们不引入匀速圆周模型，尝试只用万有引力公式导出运动方程。
设大质量天体质量为 $M$，小质量天体质量为 $m$，以大质量天体为参考系，小质量天体的初速度为$v_0=\begin{bmatrix}v_x\\v_y\end{bmatrix}$，初位置为$r_0=\begin{bmatrix}x_0\\y_0\end{bmatrix}$ ，求小质量天体的运动轨迹。

大雾中的万有引力公式：

$$\mathbf{F} = \frac{GMm}{\mathbf{r}^2}\hat{\mathbf{r}}$$

计算拉氏量并代入欧拉-拉格朗日方程

$$T = \frac{1}{2}m(\dot{r}^2+(r\dot{\theta})^2)$$ $$U = -\frac{G(M+m)m}{r}$$ $$L = \frac{1}{2}m(\dot{r}^2+(r\dot{\theta})^2)-\frac{G(M+m)m}{r}$$

得到微分方程组：

$$\left\{\begin{array}{c} \ddot{\mathrm{r}}-\mathrm{r} \ddot{\theta}^{2}=-\frac{\mathrm{G}(\mathrm{M}+\mathrm{m})}{\mathrm{r}^{2}}\\ \mathrm{r} \ddot{\theta}+2 \dot{\mathrm{r}} \dot{\theta}=0 \end{array}\right.$$

设 $l=mr^2\dot{\theta}$，则求导后 $\dot{l}=mr(r\ddot{\theta}+2\dot{r}\dot{\theta})=0$，显然角动量守恒

下面求解方程组，令 $u=\frac{1}{r}$ 换元得到

$$\frac{\mathrm{d}^{2} u}{\mathrm{d} x^{2}}+u=\frac{G(M+m) m^{2}}{l^{2}}$$

这是常系数非齐次线性微分方程，解之得：

$$u=\frac{G(M+m) m^{2}}{l^{2}}+\varepsilon \cos \left(\theta-\theta_{0}\right)$$ $$r=\frac{1}{\frac{G(M+m) m^{2}}{l^{2}}+\varepsilon \cos \left(\theta-\theta_{0}\right)}$$

其中 $\varepsilon$，$\theta_0$ 均为任意常数。所以运动轨迹是圆锥曲线。设:

$$c=\frac{G(M+m) m^{2}}{l^{2}}$$ $$r_{0}=\sqrt{x_{0}^{2}+y_{0}^{2}}$$

将所有初值带入得到：

$$\theta_{0}=\arctan \left(-\frac{\left(\frac{1}{r_{0}}-c\right)v_x+c\left(v_{y} \frac{x_{0} y_{0}}{r_{0}{ }^{2}}+v_{x} \frac{x_{0}{ }^{2}}{r_{0}{ }^{2}}\right)}{\left(\frac{1}{r_{0}}-c\right)v_y+c\left(v_{x} \frac{x_{0} y_{0}}{r_{0}{ }^{2}}+v_{y} \frac{y_{0}{ }^{2}}{r_{0}{ }^{2}}\right)}\right)$$ $$\varepsilon=\frac{1-c r_{0}}{x_{0} \cos \theta_{0}+y_{0} \sin \theta_{0}}$$

整理得到最后的式子：

$$\rho=\frac{1}{\frac{G(M+m) m^{2}}{l^{2}}+\varepsilon \cos \left(\theta-\theta_{0}\right)}$$

其中

$$\theta_{0}=\arctan \left(-\frac{\left(\frac{1}{r_{0}}-\frac{G(M+m) m^{2}}{l^{2}}\right)v_x+\frac{G(M+m) m^{2}}{l^{2}}\left(v_{y} \frac{x_{0} y_{0}}{r_{0}{ }^{2}}+v_{x} \frac{x_{0}{ }^{2}}{r_{0}{ }^{2}}\right)}{\left(\frac{1}{r_{0}}-\frac{G(M+m) m^{2}}{l^{2}}\right)v_y+\frac{G(M+m) m^{2}}{l^{2}}\left(v_{x} \frac{x_{0} y_{0}}{r_{0}{ }^{2}}+v_{y} \frac{y_{0}{ }^{2}}{r_{0}{ }^{2}}\right)}\right)$$ $$\varepsilon=\frac{1-\frac{G(M+m) m^{2}}{l^{2}} r_{0}}{x_{0} \cos \theta_{0}+y_{0} \sin \theta_{0}}$$

在其中的其中

• 当$|\varepsilon| > | \frac{G(M+m) m^{2}}{l^{2}} |$，轨迹为双曲线
• 当$|\varepsilon| = | \frac{G(M+m) m^{2}}{l^{2}} |$，轨迹为抛物线
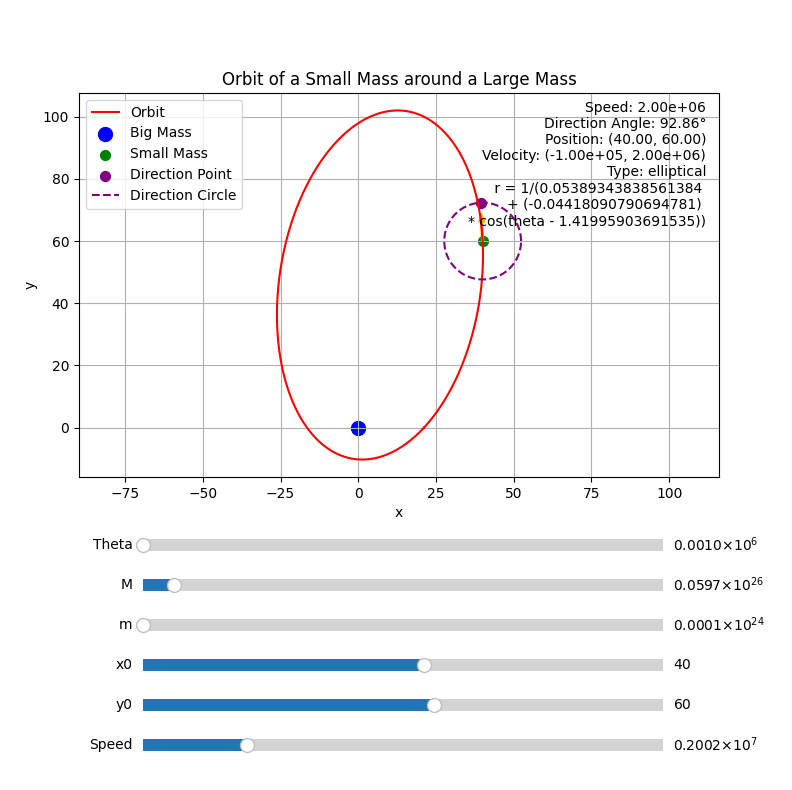
• 当$|\varepsilon| < | \frac{G(M+m) m^{2}}{l^{2}} |$，轨迹为椭圆

使用如下的仓库中的代码可以模拟及验证行星运动时的轨迹

https://github.com/feipiao594/Simple-Planet-Orbit

显示双曲线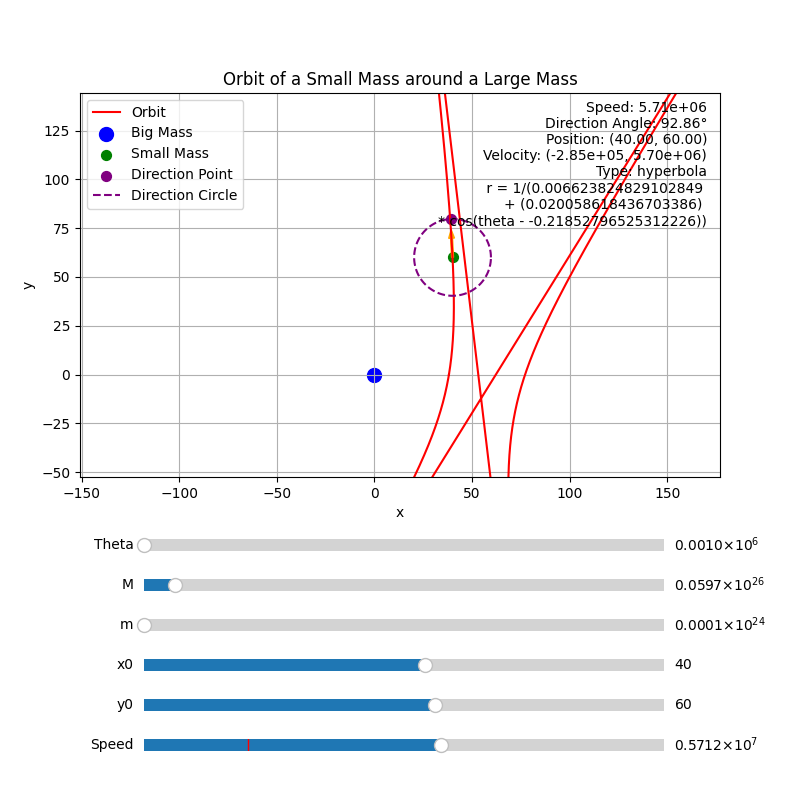

显示椭圆