离散与连续傅里叶变换之间的联系

在复习这学期的数字信号处理的时候，发现我的数字信号处理书对此的解释我完全看不懂啊，所以就花了几天时间自己推了一点公式，通过了解这些离散啊，连续啊什么的傅里叶变换的数学性质能比较直观的帮助我理解这科目到底在干什么，具体为什么要这么干

我用到的这本书上说，DTFT在信号与系统中有学，所以略讲，信号与系统里提都没提DTFT 而且我觉得DTFT还非常容易和DFT混，如果不是真去尝试证明真不清楚其中是什么含义

DTFT

想要理解DTFT得先从实际的采样开始，采样就是每隔采样周期T取一个值，就是把一个连续的信号在时间域上离散化，或者用数学一点的说法，用这种方法把一个定义在$\mathbb{R}$(时间是实数)上的函数映射成一个数列(定义在$\mathbb{Z}$上的函数)

所以这里的连续信号中的连续并不是说的数学上的函数连续，而是指定义域不是$\mathbb{R}$)

其表达式为

$x[n]=x_a(nT)$

很容易就会想知道对$x[n]$进行DTFT和对$x_a(t)$进行CTFT(连续傅里叶变换)之后的结果有什么关系

我们把两个变换的定义的式子写出来

$\mathrm{CTFT}[x(t)]=\int_{-\infty}^{+\infty}x(t)e^{-j\omega t}dt$ $\mathrm{DTFT}[x[n]]=\sum_{n=-\infty}^{+\infty}x[n]e^{-j\omega n}$

首先要说明一下我这边的符号，比如$\mathrm{DTFT}[x[n]] (\omega)$的含义是先对$x[n]$进行离散时间的傅里叶变换后的频域函数代入$\omega$，比如$\mathrm{DTFT}[x[n]] (\pi)$就是$x[n]$的频域函数代入$\pi$，这里之所以不使用$X(e^{j\omega})$这种符号是我觉得在数学上不够直观，虽然书上会说写成这种复合函数的形式有工程上的好处，但其实不方便从理论的角度去考虑，多一层不如少一层

可以看出他俩其实很相似，所以我们很容易就能联想到下面这个等式

Lemma 1:

$\mathrm{CTFT}[x(t)\cdot \delta_T(t)]=\mathrm{DTFT}[x[n]](T\omega)$

其中 $\delta_T(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT)$ ，这是采样函数，画成图像就是在坐标轴上从原点出发每隔时间T就是一个冲激

Proof:

$\begin{aligned} \mathrm{CTFT}[x(t)\cdot \delta_T(t)] &=\int_{-\infty}^{+\infty}x(t) \delta_T(t)e^{-j\omega t}dt\\ &=\int_{-\infty}^{+\infty}x(t)\sum_{n=-\infty}^{+\infty}\delta(t-nT)e^{-j\omega t}dt\\ &=\sum_{n=-\infty}^{+\infty}\int_{-\infty}^{+\infty}x(t)\delta(t-nT)e^{-j\omega t}dt\\ &=\sum_{n=-\infty}^{+\infty}x(nT)e^{-j\omega nT}\\ &=\sum_{n=-\infty}^{+\infty}x[n]e^{-jT\omega n}\\ &=\mathrm{DTFT}[x[n]](T\omega) \end{aligned}$

那么输入的函数关系怎么样已经找出来了，输出的频域函数两个变换又有什么关系呢?
首先再来算一个东西

Lemma 2:

$\mathrm{CTFT}[x(t)\cdot \delta_T(t)]=\frac{1}{T}\sum_{n=-\infty}^{+\infty}\mathrm{CTFT}[x(t)](\omega-\frac{2\pi n}{T})$

Proof:

首先对 $\delta_T(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT)$ 进行傅里叶级数展开，得到

$\delta_T(t)=\frac{1}{T}\sum_{n=-\infty}^{+\infty}e^{j\frac{2\pi n}{T}t}$

将这个式子代入连续傅里叶变换的定义式，得到

$\begin{aligned} \mathrm{CTFT}[x(t)\cdot \delta_T(t)] &=\int_{-\infty}^{+\infty}x(t) \delta_T(t)e^{-j\omega t}dt\\ &=\frac{1}{T}\int_{-\infty}^{+\infty}x(t)\sum_{n=-\infty}^{+\infty}e^{jn\omega t}e^{-j\omega t}dt\\ &=\frac{1}{T}\sum_{n=-\infty}^{+\infty}\int_{-\infty}^{+\infty}x(t)e^{j(\frac{2\pi n}{T}-\omega) t}dt\\ &=\frac{1}{T}\sum_{n=-\infty}^{+\infty}\mathrm{CTFT}[x(t)](\frac{2\pi n}{T}-\omega) \end{aligned}$

可以看到，对原本的连续信号的采样进行连续傅里叶变换得到的结果是原本信号的傅里叶变换的结果在频率轴上移动$\frac{2\pi}{T}$的整数倍得到的所有函数的和的$\frac{1}{T}$倍，这就是所谓的周期延拓

好了，由上面得到的两个小等式联立一下可以证明我们需要的东西了

Equation:

$\mathrm{DTFT}[x[n]](T\omega)=\frac{1}{T}\sum_{n=-\infty}^{+\infty}\mathrm{CTFT}[x(t)](\omega-\frac{2\pi n}{T})$

将两边的$\omega$同时换元成$\frac{\omega}{T}$，再把换元后左式多余的$(\omega)$删掉，就是，就能得到最终的式子了

$\mathrm{DTFT}[x[n]]=\frac{1}{T}\sum_{n=-\infty}^{+\infty}\mathrm{CTFT}[x(t)](\frac{\omega-2\pi n}{T})$

用人话翻译一下这个句子，对一个离散信号进行DTFT，等价于对它采样前的连续信号进行周期延拓(连续傅里叶变换后的结果在频率轴上移动$\frac{2\pi}{T}$的整数倍得到的所有的无穷多个函数的叠加的$\frac{1}{T}$倍)后再把整个频谱函数沿着频率轴放大T倍
或者说你也可以理解为采样前的连续信号先沿频率轴放大T倍在进行周期延拓
再或者你还能理解为原连续信号的周期延拓完了之后把他沿频率轴放缩到以$2\pi$为周期(DTFT它是关于$2\pi$成周期的，你可以从这个等式里一目了然的看见，也能从DTFT的定义式中证明这个)

那么你就可以理解DTFT诞生的原因了，本质上它也是一种近似获得连续信号的傅里叶变换的手段，只不过算出来的结果是原本连续傅里叶变换的移位之后又压缩了一下再叠加嘛。

从这里你就知道什么叫混叠了，在一些比较良好的情况下，比如去DTFT一个带限信号的采样，带限信号是在频率上截止频率为$\omega_c$的信号，就是说$|\omega|\ge\omega_c$时，$X(\omega)=0$，那么，既然DTFT是原函数的周期延拓，对于带限的信号来说，根据上面的等式，你可以看到下图中一个小尖坡的影响范围是$\omega_cT$，而每$2\pi$的范围内，就有两个小尖坡在影响，要想他们不重叠，自然就要求$\omega_c T \le \frac{2 \pi}{2}$，把采样周期写成采样频率即$T=\frac{1}{\omega_s}$，代入就得到了$\omega_s \ge 2\omega_c$，这不就是奈奎斯特采样定律么，在满足这个条件的情况下，DTFT结果的$[-\pi,\pi]$的部分完全就是CTFT做了一些就简单的变换，换言之，你可以通过计算DTFT，在只存储采样后的离散的数据的情况下计算出原本信号的CTFT，这就是DTFT存在的目的，如果不满足这个条件，小尖坡就会变粗，接着叠起来，就不能从DTFT获得CTFT的信息了

所以你现在明白了所谓奈奎斯特采样定律就是从采样后离散信号的DTFT能约等于看作是原本连续信号的CTFT的”约等于”能成立的需要的条件

DFT/FFT

FFT本质就是一个DFT的快速算法，就是另一种计算DFT的方法，和DFT完全没有区别，唯一需要注意的是要会用就行了，简单来说就是背下来那个蝶形图是怎么个画法

而DFT就更有趣了，先看看它的定义式

$\mathrm{DFT}[x[n]]=\sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}kn}，0\le k\le N-1$

这里没有写成$W^{-j(2\pi/N)}$也是出于这样能更加好的看出其原本的数学性质的目的

它和DTFT只有一点点差别，首先它对$x[n]$有要求，它必须是一个有限长序列，长度为N，在这样的情况下，这个序列进行DTFT，其实求和号上的差别就没了，那剩下的就只有指数上的差别了，那么其实完全满足这样的式子

$\begin{aligned}\mathrm{DFT}[x[n]](k)&=\sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}kn}\\ &=\mathrm{DTFT}[x[n]](\frac{2\pi}{N}k)，0\le k\le N-1 \end{aligned}$

这下看懂了，对一个有限长序列进行DFT就是在对它进行DTFT后$[0,2\pi]$的部分再采样N个点呢

还没完，如果你给这个长度为N的有限长序列$x[n]$后面再填M个0，让他变成长度为N+M的有限长序列$x’[n]$呢？表达式就变成了如下

$\begin{aligned}\mathrm{DFT}[x'[n]](k)&=\sum_{n=0}^{N+M-1}x[n]e^{-j\frac{2\pi}{N+M}kn}\\ &=\sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N+M}kn}\\ &=\mathrm{DTFT}[x[n]](\frac{2\pi}{N+M}k)，0\le k\le N+M-1 \end{aligned}$

好嘛，就是没添加0之前的结果采样的更加密集了一点，只要你M取特别特别大，你就可以用DFT完全逼近这个有限长序列的DTFT了，例子如下

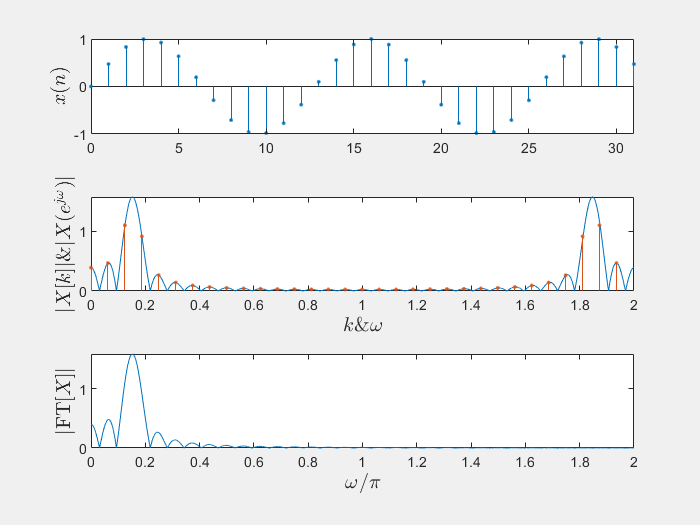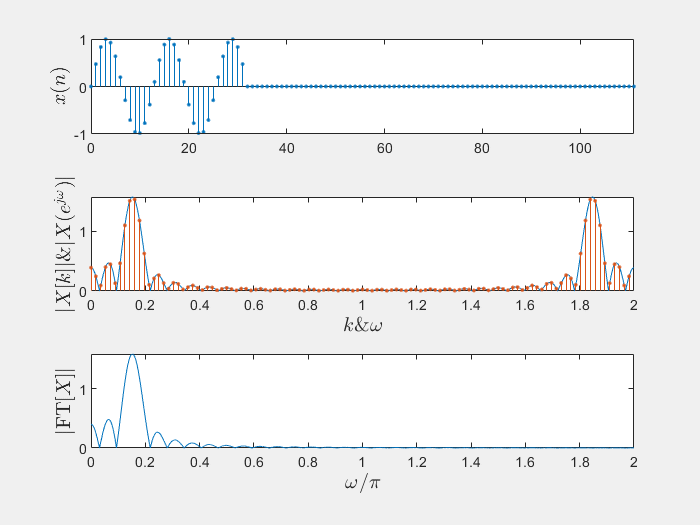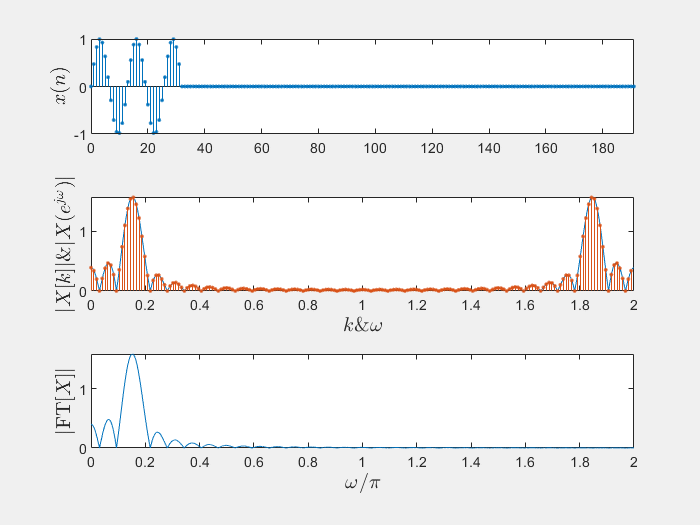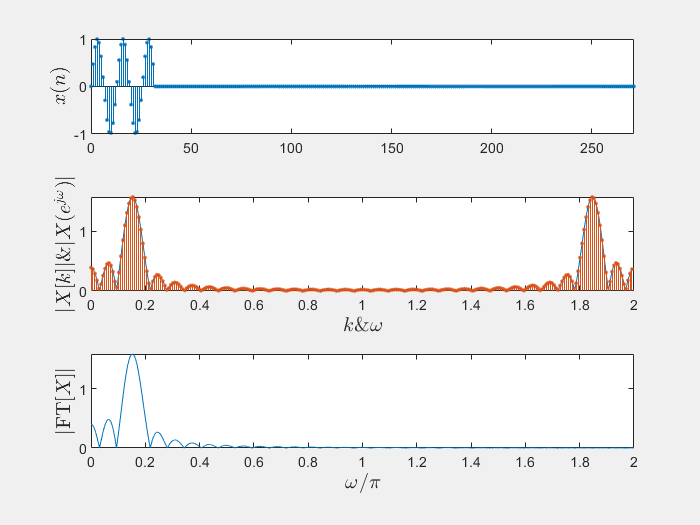
上图的matlab代码如下

pic_num = 1;   
for k=0:4:240
    s=figure(1);
    N=32;
    n=0:N-1;
    x=sin(5*n*pi/N);% 取样计算持续0到pi的sin(5t)信号
    x=[x,zeros(1,k)];
    n=0:N-1+k;
    w=linspace(0,2*pi,10000);
    y1=x*exp(-j*n'*w)/N*pi;% DFT
    y2=j*pi*((1-exp(-j*(w/pi*N+5)*pi))./(j*(w/pi*N+5))-(1-exp(-j*(w/pi*N-5)*pi))./(j*(w/pi*N-5)))/(2*pi);% DTFT
    subplot(3,1,1);stem(n,x,'.');ylabel('$x(n)$','interpreter','latex','fontsize',12);xlim([0 N-1+k]);
    subplot(3,1,2);plot(w/pi,abs(y1));hold on;
    stem(n*2*(N-2+k)/(N-1+k)/(N-1+k),abs(fft(x)/N*pi),'.');xlabel('$k \& \omega$','interpreter','latex','fontsize',12);ylabel('$|X[k]| \& |X(e^{j\omega})|$','interpreter','latex','fontsize',12);xlim([0 2]);hold off;
    subplot(3,1,3);plot(w/pi,abs(y2));xlabel('$\omega/\pi$','interpreter','latex','fontsize',12);ylabel('$|\mathrm{FT}[X]|$','interpreter','latex','fontsize',12);
    drawnow;F=getframe(s);I=frame2im(F);[I,map]=rgb2ind(I,256);
    if pic_num == 1
        imwrite(I,map,'test.gif','gif', 'Loopcount',inf,'DelayTime',0.1);
    else
        imwrite(I,map,'test.gif','gif','WriteMode','append','DelayTime',0.1);
    end
    pic_num = pic_num + 1;
end

所以，求有限长序列的DFT也是约等于求它的DTFT，这样做的优势就是，DFT还能让结果也变得离散化，方便存储的同时还有FFT这种神奇的算法能给计算加速

总结

当带限信号满足奈奎斯特采样定律时，从采样后离散信号的DTFT能约等于看作是原本连续信号的CTFT
对于有限长序列，计算DFT就是在逼近计算DTFT函数的一部分值
所以综上，我所使用的这本教材前三章的核心目的就是告诉我，可以使用某种手段(比如滤波器等等)，利用FFT就能近似计算一个连续函数的CTFT，至于其他的都是具体的计算时的分支任务。比如设计数字滤波器，本质上就是在给采样后的信号去干连续信号一样的事情