初识量子计算

考试周瞎学，写一份初见的文档，量子计算确实很有意思

关于使用的Python库:Qiskit

可以看一手官网的介绍:

Qiskit [kiss-kit] is an open-source SDK for working with quantum computers at the level of pulses, circuits, and application modules.

我主要就使用Qiskit库进行量子计算的学习

量子计算的基础知识

这一部分讲一些基础的东西

量子比特

量子比特属于叠加态，其可以表达成基础的几个状态的线性组合，而且线性组合的系数都是复数

原因是其可以组成向量空间，其实是复希尔伯特空间，这很trival

具体的表达如下

$$\langle\psi|=a\langle 1|+b \langle 0|、|\psi\rangle = a|1\rangle + b|0 \rangle$$

左矢和右矢

右矢就是普通的向量
看起来左矢就是对偶向量

点乘

如果$|\psi\rangle$是某个例子的初始状态，则$|\langle\phi|\psi\rangle|^2$代表在$|\phi\rangle$这个状态找到$|\psi\rangle$这个状态的概率

点乘具有正交性和归一性，即

$$\langle i|j \rangle = \delta_{ij}$$

张量积

张量分析当中的基本运算

$$|\psi\rangle\otimes|\phi\rangle\equiv|\psi\rangle|\phi\rangle\equiv|\psi,\phi\rangle\equiv|\psi\phi\rangle$$

注意，张量积不满足交换律感觉这里的张量积主要用于将qubit合成为张量进矩阵格式的运算

运算满足如下方法

$$\langle\phi_1\phi_2|\psi_1\psi_2\rangle = \langle\phi_1|\psi_1\rangle_1\langle\phi_2|\psi_2\rangle_2$$

外积

外积是一种用于产生算符的运算，其定义为

$$|\psi\rangle\langle\phi|=|\psi\rangle\otimes\langle\phi|$$

纯态与混合态

纯态是指可以被一个简单向量表示的量子态
位于布洛赫球上的向量是纯态，因为他们可以被书写成

$$|\psi\rangle=\begin{bmatrix}\cos\frac{\theta}{2}\\ e^{i\phi}\sin\frac{\theta}{2}\end{bmatrix}$$

而混合态就是在布洛赫球内的向量

密度矩阵

给定一个纯态$|\psi\rangle$，其密度算符(矩阵)定义为

$$\rho=|\psi \rangle \langle \psi|$$

量子逻辑门

对量子的逻辑运算可以被理解为张量乘法，即可以把量子逻辑门理解为一个矩阵运算，利用量子逻辑门计算一次的计算，由于叠加态的存在，可以同时处理很多情况，因此达到快于经典计算机的速度

量子电路要求总是可逆电路

量子逻辑门的物理实现中经常提到了一个结构，约瑟夫森结，这是组成量子逻辑门的一个重要元件

例子

import numpy as np
from qiskit import QuantumCircuit
import matplotlib.pyplot as plt
from qiskit import Aer
from qiskit.visualization import plot_state_city

circ = QuantumCircuit(3)
circ.h(0)
circ.cx(0, 1)
circ.cx(0, 2)
circ.h(2)

backend = Aer.get_backend("statevector_simulator")
job = backend.run(circ)
result = job.result()
outputstate = result.get_statevector(circ, decimals=3)
plot_state_city(outputstate)
# 注意，生成的是密度矩阵而不是直接告诉我值的虚实部
# 注意，|\psi| = a|1>+b|0>的系数a，b是复数而非实数
# 因为这个是在一个复希尔伯特空间上
# 右矢是向量，左矢是对偶向量
plt.show()

上述代码对应的量子电路图如下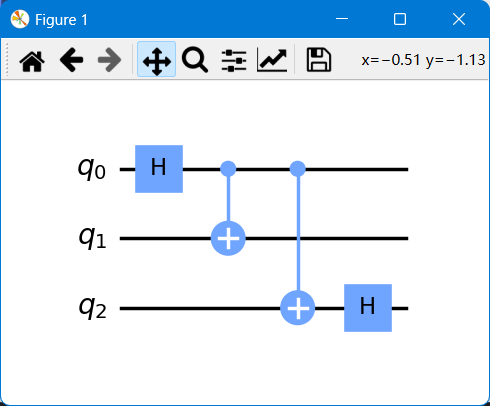

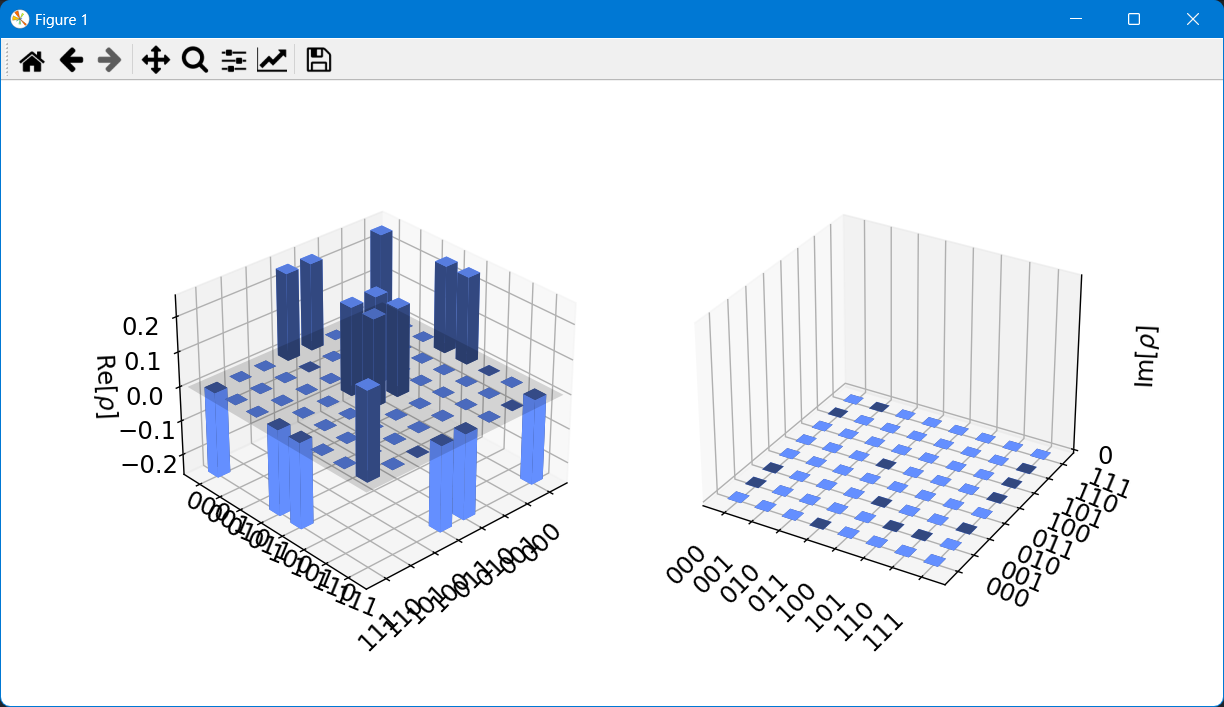
输出的结果图如下