数学实验综合练习

这里是我大一数学实验课的综合练习一的题解

题目_新冠疫情预测

搜集全球新冠疫情的数据，选择全球数据或者某一个国家的数据，研究数据的函数类型，根据全球或者某一国家截止2022年5月底的数据，预测全球(或者该国家)感染的最终规模，判断全球(或者该国家)疫情何时结束。

实验过程

我们小组将课题定为对全球新冠疫情的预测。小组将统计范围放在全球，以便对新冠疫情的分析更具全局性和准确性。实验主要分为三个步骤，首先由小组成员ds进行全球新冠疫情数据的收集整理和汇总，将其交由成员zxy，根据收集的数据研究分析其函数类型，并以此预测全球感染的最终规模和结束时间，最后由成员cj将本次实验过程、结果总结并撰写为报告。

数据搜集阶段

对于全球疫情数据的收集，由于数据的庞大及专业性，显然难以以线下的调查或者查阅资料获得，所以小组将目光投向网络。根据实验要求，所需的数据是全球范围内截止2022年5月的疫情病例人数。小组划定起始时间为2020年1月，以月为单位，收集了29个月的新冠感染数据。我们小组采用以ChatGPT收集数据为准。整理合并制作出数据表格，如下图

数据分析及疫情预测阶段

根据收集的全球病例数据，通过Matlab制作出了散点图，如下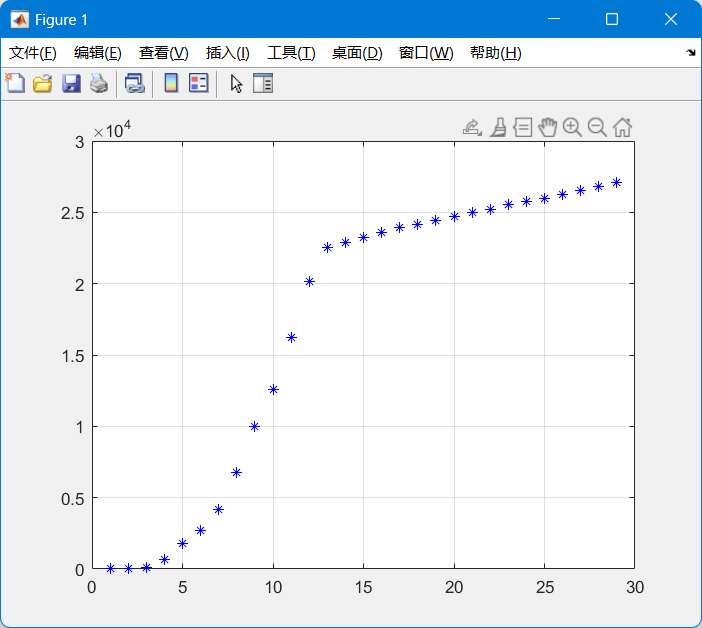

由图可见，感染总数从初始阶段开始便猛增，增长速率也在加快，而后半段呈现类线性的缓慢上升，显然这不符合书本上已给出的数学模型。经小组思考和讨论后，决定将其分为两段分别研究。
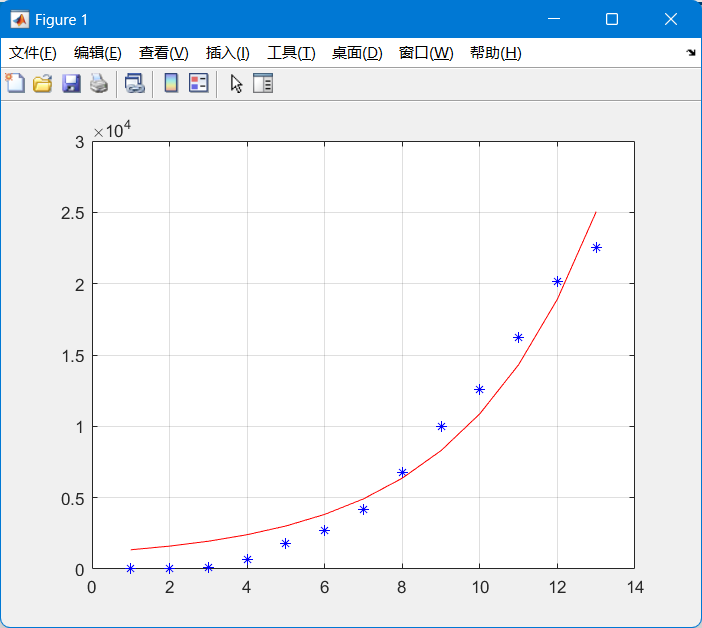
前半部分是J型曲线模型
模型公式如下

$$N(t)=N_0(1+e^{kt})$$

代码如下

clc;clear;
y=[0.09,0.85,86.74,682.41,1795.69,2717.62,4174.10,6735.730,10001.90...
,12581.53,16234.30,20174.37,22554.55];
x=1:length(y);
a=[500,2];
f = @(a,x)a(1)*(1+exp(a(2)*x));
[A,resnorm] = lsqcurvefit(f,a,x,y);
plot(x,y,'b*');
hold on;
X=1:13;
Y=A(1).*(1+exp(A(2)*X));
plot(X,Y,'r-');
grid on;

后半部分为logist模型
模型公式如下

$$N(t)=\frac{c}{1+ae^{kt}}$$

代码如下

clc;clear;
y=[22911.44,23250.81,23594.19,23923.71,24156.30,24395.02,24703.13...
,25000.68,25211.07,25519.78,25768.44,25941.22,26241.14,26526.19,26799.18,27099.82];
x=1:length(y);
a=[5000,100,1];
f = @(a,x)a(1)./(1+a(2)*exp(-a(3)*x));
[A,resnorm] = lsqcurvefit(f,a,x,(y-22911));
plot(x,y,'b*');
hold on;
X=1:40;
Y=A(1)./(1+A(2)*exp(-A(3)*X))+22911;
plot(X,Y,'r-');
grid on;

分别利用lsqcurvefit拟合非线性函数，最终得到前者的系数组成的数组A为

$$A = \quad 1.0e+03\quad * \quad [4.4978 \quad 0.0128 \quad 0.0003]$$

后者的系数组成的数组A为

$$A = [576.7970 \quad 0.2883]$$

经小组共同研究，发现主要是前半段的模型与logist模型差异较大，观察其图形，与物种增长的J型曲线极为相似。小组推测出现这种曲线的原因是，新冠病毒爆发的初期，大多国家并没有采取有效的控制措施，对抗病毒的药物或是疫苗任然处于研制当中，此时的新冠病毒就处于没有任何威胁的环境中，因而其增长曲线与J型极为类似，而与logist模型相悖。

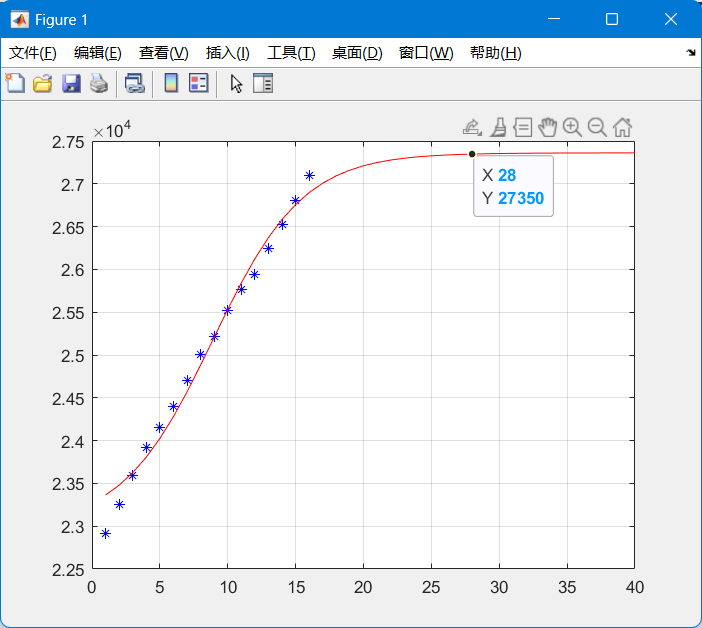
由后半段的拟合曲线图可看出，感染人数的变化趋势与书本上所给例子有相似之处。两段曲线的分界点为2021年12月，小组判断在此时疫情已经得到了一定的控制，同时病毒的致病能力也会有所下降，从而逐渐符合logist模型。

最终结果

根据拟合模型预估(即第四张图中 X:28，Y:27350)，全球疫情将持续长达4年左右，最终感染规模为2.74亿人，预计在2023年5月彻底结束。