CSAPP章节二中的数学公式整理

这一章偏向理论，有时候能利用编码知识大大简化计算之类的

关于这一章的符号说明:

注意：当反函数难以直观写出时，将直接省略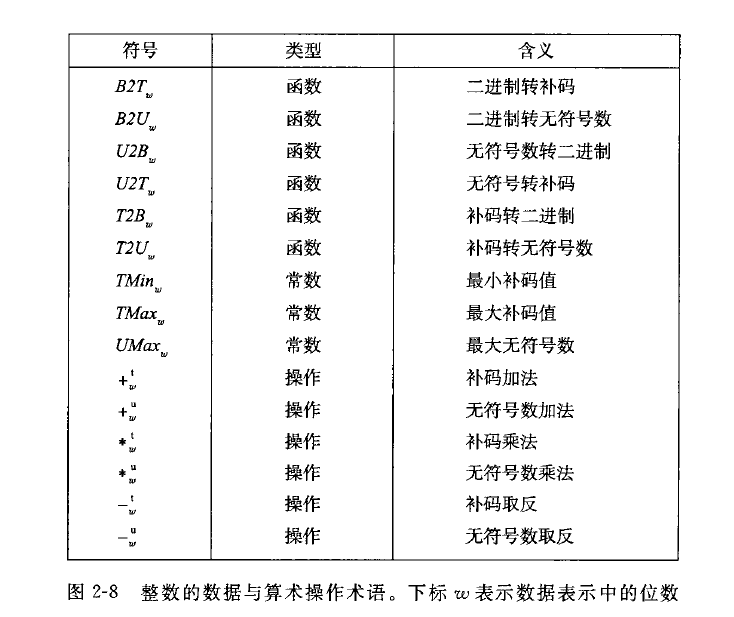

整数部分:

1.二进制转反码

$$B 2 S_{w}(\vec{x}) \doteq(-1)^{x_{w-1}} \cdot\left(\sum_{i=0}^{w-2} x_{i} 2^{i}\right)$$

2.二进制转原码

$$B2O_{w}(\vec{x}) \doteq-x_{w-1}\left(2^{w-1}-1\right)+\sum_{i=0}^{w-2} x_{i} 2^{i}$$

3.二进制转补码

补码有特殊的数学性质，形成一个自洽的体系，故如今机子几乎都用补码
这是一个一一到上的映射，故对应0的向量x不像原码一般对0有两种解释

$$B 2 T_{w}(\vec{x}) \doteq-x_{w-1} 2^{w-1}+\sum_{i=0}^{w-2} x_{i} 2^{i}$$

4.补码转无符号

二进制（向量x）不变的直接编码转化，公式很简单

$$T 2 U_{w}(x) \doteq B 2 U_{w}\left(T 2 B_{w}(x)\right)$$ $$T 2 U_{w}(x)=\left\{\begin{array}{ll} x+2^{w}, & x<0 \\ x, & x \geqslant 0 \end{array}\right.$$ $$B 2 U_{w}\left(T 2 B_{w}(x)\right)=T 2 U_{w}(x)=x+x_{w-1} 2^{w}$$

5.无符号转补码

同上，二进制（向量x）不变的直接编码转化

$$U 2 T_{w}(x) \doteq B 2 T_{w}\left(U 2 B_{w}(x)\right)$$ $$U 2 T_{w}(u)=\left\{\begin{array}{ll} u, & u \leqslant \operatorname{TMax}_{w} \\ u-2^{w}, & u>\operatorname{TMax}_{w} \end{array}\right.$$

6.二进制转无符号

$$B 2 U_{w}(\vec{x}) \doteq \sum_{i=0}^{w-1} x_{i} 2^{i}$$

7.补码的相关性质（无符号省略）

存在有定义域 $[TMin,TMax]$ ,其中满足
$\mid \text { TMin }|=| \text { TMax } \mid+1$

$$\operatorname{TMin}_{w}\doteq-2^{w-1}\operatorname\qquad{TMax}_{w} \doteq \sum_{i=0}^{w-2} 2^{i}=2^{w-1}-1$$

8.整数的扩展

无符号零扩展，即直接在二进制下的数字前补零，在16进制下也是补0

补码的符号扩展，即在二进制下补原先符号的数字，若为正数补1，负数补0，在16进制下前者补f后者补0

相关公式

$$B 2 T_{w+k}\left([\underbrace{x_{w-1}, \cdots, x_{u-1}}_{k 个数}, x_{u-1}, x_{w-2}, \cdots, x_{0}]\right)=B 2 T_{w}\left(\left[x_{u-1}, x_{w-2}, \cdots, x_{0}\right]\right)$$

9.整数的截断数字

• 无符号
  这里所谓的截断数字对于二进制来说就单纯是把多出来的高位切掉而已
  令 $\vec{x}$ 等于位向量 $\left[x_{w-1}, x_{w-2}, \cdots, x_{0}\right] $, 而 $ \vec{x}^{\prime}$ 是将其截断为 k 位的结果: $\vec{x}^{\prime}=\left[x_{k-1}\right.$ , $ \left.x_{k-2}, \cdots, x_{0}\right]_{\text {。 }} $令$ x=B 2 U_{w}(\vec{x}), x^{\prime}=B 2 U_{k}\left(\vec{x}^{\prime}\right) $ 。则 $x^{\prime}=x \bmod 2^{k}$ 。

  $$x^{\prime}=x \bmod 2^{k}=x-\sum_{i=k+1}^{w}{x_i}2^{i}$$

• 补码
  这里所说的截断的定义是借由无符号数的截断，即先转化为对应的无符号数，再进行截断
  实质上对于二进制来说也是直接的高位截断
  令 $\vec{x}$ 等于位向量 $\left[x_{w-1}, x_{w-2}, \cdots, x_{0}\right]$ , 而 $\vec{x}^{\prime} $ 是将其截断为 k 位的结果: $\vec{x}^{\prime}=\left[x_{k-1}\right. $ , $ \left.x_{k-2}, \cdots, x_{0}\right]$ 。令 $ x=B 2 U_{w}(\vec{x}), x^{\prime}=B 2 T_{k}\left(\vec{x}^{\prime}\right) $ 。则 $ x^{\prime}=U 2 T_{k}\left(x \bmod 2^{k}\right) $ 。

  $$x^{\prime}=U 2 T_{k}\left(x \bmod 2^{k}\right) =B 2 T_{w}(x)-\sum_{i=k+1}^{w-1}{x_i}2^{i}+{x_w}2^{w}-{x_k}2^{k}$$